§13 Cantidades hidrodinámicas en el flujo de acreción

A continuación calcularemos el campo de velocidades en el flujo de acreción descrito en la sección §1. La diferencial de la posición de una partícula en coordenadas esféricas es:

$$\mathrm{d} \vec r = \mathrm{d} r \widehat{e}_r + r \mathrm{d} \theta \widehat{e}_\theta + r \sin \theta \mathrm{d} \varphi \widehat{e}_\varphi,$$ (13.19)

donde $\widehat{e}_i$    ($i=r,\theta,\varphi$   ) $$ es un vector unitario en la dirección $i$. El valor correspondiente de la velocidad se obtiene de la ec.(1.19) dividiendo por la diferencial del tiempo $\mathrm{d}t$.

La solución al potencial central Newtoniano con energía cero, como se manifiesta en la ec.(2.3) se da a continuación (Landau & Lifshitz, 1989):

$$r = \frac{ \mathfrak{R}}{ 1 + \cos \varphi' },$$ (13.20)

donde la variable primada se refiere a las coordenada que describe la trayectoria de una partícula de fluido sobre el plano de la parábola (fig.(I.1)) y $\mathfrak{R} = \Gamma^2_$n$/ G M$, siendo $\Gamma_$n$$ el momento angular normal al plano de la trayectoria.

El material que se acreta hacia la estrella y el disco, lejos de la estrella (a la distancia $r_\infty$) tiene un momento angular $\Gamma$. A esta distancia, la velocidad de la partícula de fluido es $\vec v_\infty = \dot{\varphi} r_\infty \sin \theta_0 \widehat{e}_\varphi$. De esta manera el momento angular inicial está relacionado con el momento angular normal al plano de la trayectoria por:

$$\Gamma = \Gamma_n sen\theta_0.$$ (13.21)

Las coordenadas primadas, están relacionadas con las no primadas mediante transformaciones lineales sencillas que involucran rotaciones, de las cuales se obtiene: $\cos \varphi' = - \sin \varphi \sin \theta / \sin \theta_0$, $\sin \varphi = \tan \theta_0 / \tan \theta$. Utilizando la ec.(1.20), la trayectoria de las partículas expresada en las coordenadas no primadas es:

$$\frac{ r }{ r_\text{d} } = \frac{ \sin^2 \theta }{ \left( 1 - \frac{ \cos \theta }{ \cos \theta_0 } \right) }.$$ (13.22)

Utilizando la ec.(1.19) y el valor del momento angular del material en acreción, así como la ec.(1.22), se encuentra fácilmente el valor de la velocidad azimutal. Con esta última y la ec.(2.3) se obtiene entonces el campo de velocidades (Ulrich, 1976):

$$v_ = - \left( \frac{ G M }{ r } \right) ^{ 1 /2 } \left( 1 + \frac{ \cos \theta }{ \cos \theta_0 } \right)^{ 1 / 2 },$$

$$v_\theta = \left( \frac{ GM }{ r } \right) ^{ 1 / 2 } \frac{ \cos... ...sin \theta } \left( 1 + \frac{ \cos \theta }{ \cos\theta_0 } \right)^{ 1 / 2 },$$

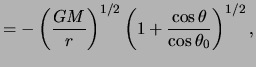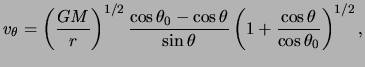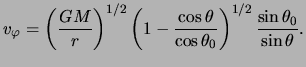$$v_\varphi = \left( \frac{ G M }{ r } \right)^{ 1 / 2 } \left( 1 -... ...heta }{ \cos \theta_0 } \right)^{ 1 / 2 } \frac{ \sin \theta_0 }{ \sin \theta}.$$ (13.23)

Para encontrar el campo de densidades utilicemos la conservación de masa a través de un tubo de corriente, es decir:

$$\rho \vec v \cdot \mathrm{d} \vec a \bigg \vert _{ r = r_\infty } = \rho\vec v \cdot d\vec a \bigg \vert _{r},$$ (13.24)

donde el elemento de área está dado por:

$$\mathrm{d} \vec a = r^2 \sin \theta \mathrm{d} \theta \mathrm{d} ... ...varphi \widehat{e}_\theta + r \mathrm{d}r \mathrm{d}\theta \widehat{e}_\varphi.$$ (13.25)

Como hemos supuesto hasta ahora, lejos de la estrella el material se acreta hacia la estrella de manera uniforme y constante en el tiempo, por lo que:

$$\dot{M} = 4 \pi \rho_\infty \vert v_r \vert r^2_\infty = ,$$ (13.26)

donde $\dot M$ representa la tasa de acreción. Por otra parte, para un radio fijo, de la ec.(1.22) se obtiene que:

$$\sin \theta \mathrm{d} \theta = \left\{ 1 + \zeta^{-1} \left( -1 + 3 \cos^2 \theta_0 \right) \right\} \sin \theta_0 \mathrm{d} \theta_0,$$ (13.27)

donde $\zeta = r / r_$d$$. Utilizando la ec.(1.24), eq.(1.26) y la ec.(1.27) se encuentra el valor de la densidad como función de la posición:

$$\rho = \frac{ \dot{M} }{ 4 \pi r^2 \vert v_r \vert } \left\{ 1 + \zeta^{-1} \left( -1 + 3 \cos^2 \theta_0 \right) \right\}^{-1}.$$ (13.28)